How can molecules evolve to become more complex, to the point smaller ones might eventually become large, complex, biological entities? When molecules are copied, it is too easy for the smaller ones to outcompete the larger ones because fewer steps are needed to copy the smaller ones. So, the ones that can be copied faster win the evolutionary race.
In 1967, the molecular biologist Sol Spiegelman took RNA from a bacteriophage, which is a virus that infects bacterial cells, and used special enzymes to get the RNA to evolve. What the enzymes do is to produce more copies of the RNAs that are in the tube, but as all things around us – they do so imperfectly (if there wasn’t this imperfection then no Darwinian evolution could take place at all, either in this tube or around us).
After a while, a small sample was moved to a new tube and the process was repeated. After more than 70 such repeats (equivalent to 70 generations) the original sequence of about 4500 bases long became significantly smaller – only about 220 bases long. The faster replication of shorter and shorter RNAs leads to such a small RNA that it earned the name ‘Spiegelman’s Monster’.
Spiegelman’s Monster leads us to wonder, if small molecules win, then why aren’t all molecules vanishingly small? How did we get complexity in molecules at all (with RNA, RNA and proteins being prime examples of complex molecules)? Researchers have now shown how chemical self-replicators can become more complex, in what may be a step towards beating the complexity monster.
The group of Sijbren Otto from the University of Groningen in The Netherlands previously found a special kind of molecule that can self-replicate by self-assembling. These simple molecules are composed of rings of carbon and hydrogen, called benzenes, along with two “arms” and a “tail”. The arms are thiol groups (molecules containing sulfur) that can form a type of bond called a “disulfide bond” with other thiol arms under regular laboratory conditions. The “tails” are extremely short strings of amino acids, like a simple protein.
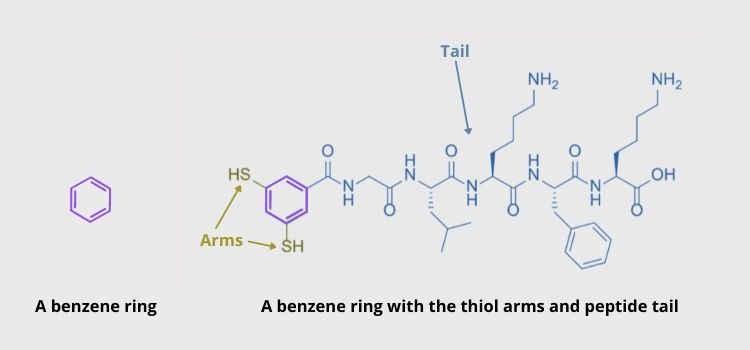
The molecule on the right is a normal benzene ring. The molecule on the left is the building block used in this study, which is based on a benzene ring. Image Source: Paper authors and Sciworthy
These building blocks form a “ring of rings,” typically composed of three to six benzene units connected by those disulfide arms. Rings of all sizes are dynamically interconverting by exchanging building blocks, in a disulfide exchange reaction. It was found that a particular ring size can self-assemble when rings of identical size stack on top of each other to form fibers. As more and more of those rings stack onto the fibers, the fibers become longer and longer.
This process is actually catalyzed by the fiber’s edges themselves. You can see this for yourself with this animation. Under mechanical agitation, such as stirring, long fibers tend to break and produce more fibers which further drives the stacking of more rings onto fibers, until eventually all the molecules of the particular size are converted into fibers. All of this means that the rings are self-replicators — they can make copies of themselves without the help of other enzymes.
Next, they discovered that two replicators with different ring sizes (such as rings of three and rings of six) can both replicate in a specific environment. Not surprisingly, the simpler three-ring replicators have an advantage over the complex six-ring replicators during the replication process. This is because the smaller rings are easier to make. Is there a way to propagate the slow and complex six-ring replicators? In other words, can we beat the Spiegelman’s Monster?
It turned out the answer has to do with a basic principle of biology called “equilibrium.” The three-ring replicators indeed replicate faster because they are structurally simpler, but it also means they would be destroyed faster. If the system is continuously undergoing replication and destruction processes, then the complex six-ring replicator may have a chance to win.
Remember this from high school bio? No? It’s okay. This is a graphical representation of what “equilibrium” means, in a general sense. But it can apply to more than just water molecules! Source: Bio Libre Texts
To test their assumption, the Otto group performed an experiment by adding chemicals that speed up the formation of three and six-ring replicators, and also chemicals that break them down back to their building blocks. This is all happening continuously and simultaneously. Encouragingly, the six-ring replicators outcompeted the smaller three-ring replicators under this condition. The results of this experiment indicate that when the system is out-of-equilibrium (such as when molecules are being destroyed faster than they are built) the more complex molecules will prevail.
That wasn’t the whole story. While the difference in complexity between the two replicators was small, the more complex replicator was a better catalyst for some chemical reactions. So, this may be another reason why complex molecules are selected in real life.
This study solved a fundamental question in science. How are complex molecules retained during the replication process? Indeed, life is not in equilibrium, so the key here is in the out-of-equilibrium state. Life is in a dynamic state where energy is constantly being consumed to build or break down molecules. In some cases, there is more destruction and in other cases there is more construction. No sub-system of life is ever in equilibrium, as equilibrium means death. Now that the Spiegelman’s Monster has been defeated, chemists who study the origin of life are on to other challenges!


